분포 모형은 확률 변수가 가질 수 있는 값들의 빈도나 가능성을 나타내는 함수입니다. 이 함수를 통해 우리는 확률 변수가 특정 값일 확률을 예측하거나 분석할 수 있습니다. 확률 분포에는 확률밀도함수, 누적분포, 확률 질량함수와 같은 여러가지 개념이 포함되어 있습니다. 이를 통해 우리는 다양한 현상과 데이터의 분포를 설명하고 예측하는데 활용할 수 있습니다.
1. 확률 분포의 개념과 종류
확률 분포는 확률 변수의 가능한 값들과 그 값들이 나타날 확률을 나타내는 함수입니다. 데이터 분석에서 확률 분포는 중요한 개념으로, 데이터의 특성과 패턴을 파악하는 데 도움을 줍니다. 다양한 현상과 데이터를 설명하는 확률 분포의 종류가 있으며, 각각의 분포는 특정한 형태와 특징을 가지고 있습니다.
1-1. 일반적인 확률 분포: 정규분포, 이항분포, 포아송분포, 지수분포
정규분포
정규분포는 연속적인 데이터의 가장 대표적인 분포로, 종 모양을 가지는 특징을 갖습니다.
예를 들어, 인구 키, 시험 점수, 체중 등 실제 세계에서 많은 현상들이 정규분포에 가까운 분포를 따릅니다.
평균과 표준편차 두 매개변수를 통해 모양을 결정합니다.
"평균은 70, 표준편차는 10인 학생들의 시험 점수"와 같은 현상을 정규분포를 통해 모델링할 수 있습니다.

이항분포
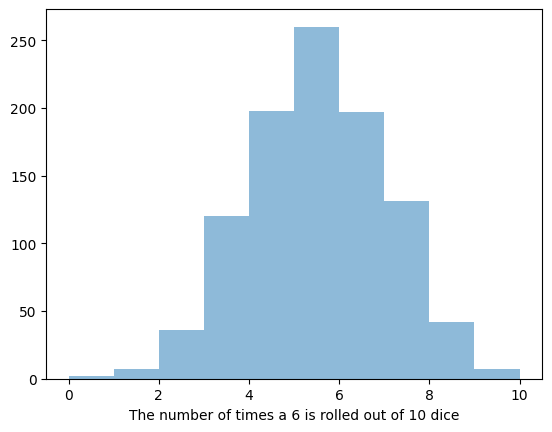
이항분포는 독립적인 시행에서 두 가지 결과, 성공과 실패, 중 하나가 나올 확률을 다룹니다.
동전 던지기와 같은 이진 결과를 분석할 때 유용합니다.
"주사위를 10번 던졌을 때 6이 나오는 횟수"와 같은 경우 이항분포를 사용하여 확률을 계산할 수 있습니다.
포아송분포
포아송분포는 사건의 발생 빈도를 나타내는 분포로, 단위 시간이나 공간에서 어떤 사건이 몇 번 일어날지 예측할 때 사용됩니다.
"하루에 평균 3번의 이메일 도착"과 같은 사건 발생 빈도를 포아송분포로 모델링할 수 있습니다.

지수분포
지수분포는 사건 발생 간격을 다루는 연속 분포로, 어떤 사건이 발생한 후 다음 사건이 발생할 때까지의 시간을 모델링합니다.
"고장난 기계의 수리 시간"이나 "고객이 매장에 도착하는 시간 간격"과 같은 사건 간격을 지수분포로 모델링할 수 있습니다.
평균 발생 시간이 주어질 때, 다음 사건이 발생할 확률을 계산할 수 있습니다.

1-2. 다양한 확률 분포: 감마분포, 베타분포, 카이제곱 분포, T분포, F분포
감마분포
- 감마분포는 양의 실수 값을 가지는 연속적인 데이터를 다루는 분포로, 양의 값만 가질 때 유용합니다.
- "제품의 수명", "서비스 시간"과 같은 양의 값을 모델링하는 데 활용됩니다.
- 형태 파라미터$($shape parameter$)$와 척도 파라미터$($scale parameter$)$를 통해 모양을 조절할 수 있습니다.
베타분포
- 베타분포는 [0, 1] 구간에서 값을 가지는 데이터를 모델링하는데 사용됩니다.
- 성공과 실패의 비율을 나타내거나, 변화하는 성공 확률 등을 다룰 때 유용합니다.
- "생산 제품의 불량률", "사용자 행동의 변화율"과 같은 데이터 분석에 활용됩니다.
카이제곱 분포
- 카이제곱 분포는 표본 분산을 추정하거나 카이제곱 검정 등에서 사용되는 분포입니다.
- 자유도$($dof, degree of freedom$)$라는 파라미터를 통해 분포의 모양이 변화합니다.
- "표본 분산", "카이제곱 검정 통계량"과 같은 분석에 활용됩니다.
T분포
- T분포는 작은 표본 크기에서 모평균의 구간 추정 및 가설 검정에 사용되는 분포입니다.
- 자유도를 통해 분포 모양이 결정되며, 표본 크기가 작을 때 더 정확한 결과를 제공합니다.
- "평균 차이의 신뢰구간 추정", "표본 평균의 가설 검정"과 같은 분석에 활용됩니다.
F분포
- F분포는 분산 비율의 가설 검정 및 분산 분석$($ANOVA$)$에서 사용되는 분포입니다.
- 두 개 이상의 그룹 간 변동과 내부 변동을 비교하는 데 유용합니다.
- "그룹 간 분산과 내부 분산 비율의 가설 검정", "여러 그룹 간 평균 차이 검정"과 같은 분석에 활용됩니다.
위의 다양한 확률 분포들은 특정 현상이나 데이터 특성에 따라 선택하여 사용할 수 있습니다. 각 분포의 특징을 파악하고 데이터와의 적합성을 평가하여 정확한 분석 결과를 얻을 수 있습니다.
'IT > AI' 카테고리의 다른 글
| [NLP] Word Embedding 기법 [기초] (0) | 2023.08.16 |
|---|---|
| [통계] Day 3-3 데이터 분포 가정과 가정 검토 (0) | 2023.08.16 |
| [통계] Day 3-1 상관 분석 (0) | 2023.08.16 |
| [통계] Day 2-3 가설 검정과 분석 방법 (0) | 2023.08.11 |


