군집 분석은 비슷한 특성을 가진 데이터를 그룹으로 분류하는 데이터 마이닝 기법입니다. 데이터의 패턴과 유사성을 파악하며 이를 기반으로 그룹 간의 차이를 이해하는데 사용됩니다. 군집 분석은 고객 세그먼테이션, 행동 패턴 분석, 이미지 처리, 생물학적 분류 등 다양한 분야에서 활용되며 데이터를 구조화하고 파악하는 중요한 도구로 사용됩니다.
1. 목적
- 데이터 탐색과 시각화: 데이터의 복잡성을 이해하고 시각화하여 구조를 파악합니다.
- 성질과 특성 파악: 데이터 그룹 간의 차이와 공통된 특성을 분석하여 인사이트를 도출합니다.
- 데이터 전처리와 변수 선택: 변수들의 중요성을 평가하고 중복되거나 불필요한 변수를 제거합니다.
- 예측 및 분류: 군집 분석을 통해 얻은 정보를 활용하여 예측 모델을 개발하거나 분류 작업에 활용합니다.
2-1. 계층적 군집 분석
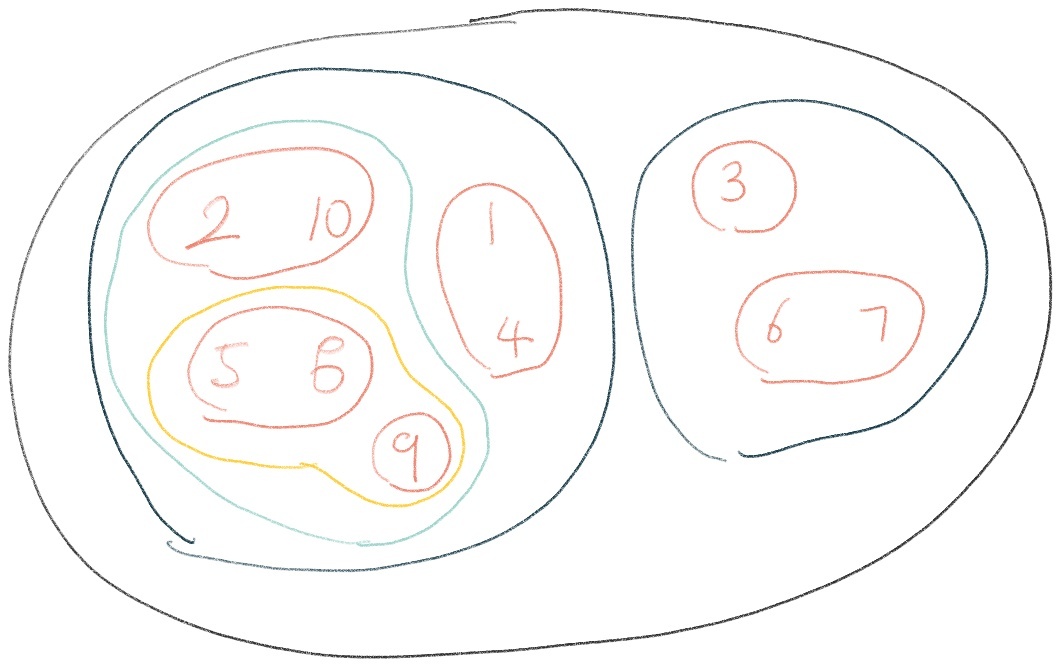
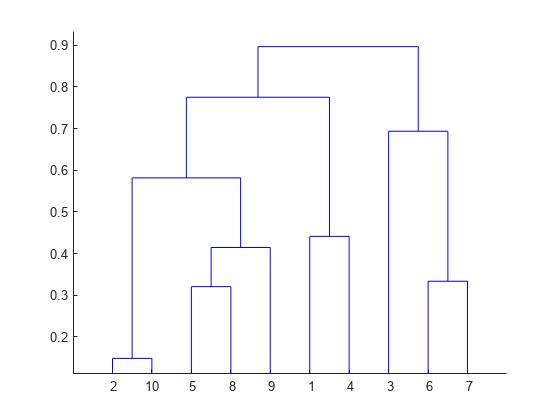
계층적 군집 분석은 유사도나 거리를 기반으로 데이터를 계층적으로 그룹화하는 기법입니다. 덴드로그램$($Dendrogram$)$을 통해 데이터 간의 계층 구조를 시각화합니다. 계층적 군집 분석은 클러스터 수를 미리 정하지 않아도 유연하게 탐색할 수 있는 장점이 있습니다.
2-2. 비계층적 군집 분석
비계층적 군집 분석은 사전에 정한 클러스터 수에 따라 데이터를 그룹화하는 방법입니다. 초기 중심값을 설정하고 데이터를 해당 클러스터에 할당한 후, 중심값을 업데이트하는 과정을 반복하여 군집을 형성합니다. 이 방법은 대용량 데이터에 대해서도 상대적으로 빠른 속도로 처리할 수 있습니다.
3. 군집 분석의 일반적인 절차
- 데이터 준비: 군집 분석에 사용할 데이터를 준비합니다.
- 거리 또는 유사도 측정: 데이터 포인트 간의 유사도나 거리를 측정합니다.
- 군집화 알고리즘 선택: 계층적 군집 분석 또는 비계층적 군집 분석 중 어떤 방법을 선택할지 결정합니다.
- 초기 군집 중심 설정: 비계층적 군집 분석의 경우 초기 중심값을 설정합니다.
- 군집화 수행: 선택한 알고리즘을 이용하여 군집화를 수행합니다.
- 군집 결과 해석: 군집 결과를 해석하고 인사이트를 도출합니다.
4. 데이터 전처리
군집 분석을 수행하기 전에 데이터를 전처리하는 것이 중요합니다. 데이터 전처리는 결과에 큰 영향을 미치며 다음과 같은 단계를 포함할 수 있습니다:
- 변수 표준화: 변수의 범위나 척도가 다를 경우, 각 변수를 표준화하여 데이터의 크기 차이를 줄입니다. 주로 Z-score나 최소-최대 스케일링을 사용합니다.
- 결측치 처리: 결측치가 있는 경우 삭제, 대체, 예측 등의 방법을 사용하여 처리합니다. 다만, 결측치 처리는 데이터 손실이나 왜곡을 유발할 수 있으므로 신중히 진행해야 합니다.
5. 거리 또는 유사도 측정
군집 분석에서는 데이터 포인트 간의 거리 또는 유사도를 측정하여 클러스터를 형성합니다. 다양한 거리나 유사도 지표를 사용할 수 있으며, 데이터의 특성에 따라 선택합니다.
- 유클리디안 거리$($Euclidean Distance$)$: 데이터 포인트 간의 직선 거리를 측정합니다.
- 맨하탄 거리$($Manhattan Distance$)$: 데이터 포인트 간의 가로세로 이동 거리를 측정합니다.
- 코사인 유사도$($Cosine Similarity$)$: 데이터 포인트 간의 각도를 측정하여 유사도를 계산합니다.
- 자카드 유사도$($Jaccard Similarity$)$: 데이터 포인트 간의 교집합과 합집합의 비율을 측정합니다.

1. 유클리디안 거리 $($Euclidean Distance$)$:
두 데이터 포인트 $p$와 $q$ 사이의 유클리디안 거리는 아래와 같이 계산됩니다.
$$\text{distance}(p, q) = \sqrt{\sum_{i=1}^n (p_i - q_i)^2}$$
여기서 $n$은 데이터 포인트의 차원을 나타내며, $p_i$와 $q_i$는 두 데이터 포인트의 해당 차원의 값을 나타냅니다.
2. 맨하탄 거리 $($Manhattan Distance$)$:
두 데이터 포인트 $p$와 $q$ 사이의 맨하탄 거리는 아래와 같이 계산됩니다.
$$\text{distance}(p, q) = \sum_{i=1}^n |p_i - q_i|$$
3. 코사인 유사도 $($Cosine Similarity$)$:
두 데이터 포인트 $p$와 $q$ 사이의 코사인 유사도는 아래와 같이 계산됩니다.
$$\text{similarity}(p, q) = \frac{p \cdot q}{\|p\| \|q\|}$$
여기서 $p \cdot q$는 두 벡터의 내적을 나타내며, $\|p\|$와 $\|q\|$는 각각 벡터 $p$와 $q$의 유클리디안 놈$($norm$)$을 나타냅니다.
4. 자카드 유사도 $($Jaccard Similarity$)$:
두 데이터 포인트 $p$와 $q$ 사이의 자카드 유사도는 다음과 같이 계산됩니다.
$$\text{similarity}(p, q) = \frac{|p \cap q|}{|p \cup q|}$$
여기서 $p \cap q$는 두 집합의 교집합을 나타내며, $p \cup q$는 두 집합의 합집합을 나타냅니다.
6. 군집화 알고리즘
다양한 군집화 알고리즘이 있으며, 데이터의 특성과 목적에 따라 선택합니다.
- K-means: 사전에 정한 클러스터 수$($K$)$에 따라 데이터를 그룹화합니다. 중심점과의 거리를 기반으로 클러스터에 할당하고 중심점을 업데이트합니다.
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 중심점 4개의 랜덤데이터 생성
data, label = make_blobs(n_samples=100, centers=4)
# K-Means 군집 분석 알고리즘
kmeans = KMeans(n_clusters=4)
kmeans.fit(data)
------------------------------------------------------------
centroids = kmeans.cluster_centers_
print(f"군집 중심점 좌표 : \n{centroids}")
for i in range(len(centroids)):
print(i, ":", len(label[label == i]))
>>>
군집 중심점 좌표 :
[[-1.93584184 8.22489586]
[-2.65643158 -9.26311534]
[ 2.36180216 0.70457966]
[-4.02678443 6.41906899]]
0 : 25
1 : 25
2 : 25
3 : 25
------------------------------------------------------------
clusters = []
for i in range(len(centroids)):
# i번째 군집에 속하는 데이터
cluster_data = data[label_predicted == i]
# 각 준집을 외부 데이터에 저장
clusters.append(cluster_data)
print(f"군집 {i+1}")
print(f"군집의 중심점 : {centroids[i]}")
print(f"데이터 개수 : {len(cluster_data)}")
>>>
군집 1
군집의 중심점 : [-1.93584184 8.22489586]
데이터 개수 : 27
군집 2
군집의 중심점 : [-2.65643158 -9.26311534]
데이터 개수 : 25
군집 3
군집의 중심점 : [2.36180216 0.70457966]
데이터 개수 : 25
군집 4
군집의 중심점 : [-4.02678443 6.41906899]
데이터 개수 : 23
------------------------------------------------------------
import matplotlib.pyplot as plt
for i, cluster in enumerate(clusters):
plt.scatter(cluster[:,0],cluster[:,1], label=f"cluster{i+1}")
plt.legend()
plt.show()>>>

- DBSCAN $($Density-Based Spatial Clustering of Applications with Noise$)$: 밀도 기반으로 클러스터를 형성하며, 밀집된 지역을 클러스터로 간주하고 이상치를 처리합니다.
- GMM $($Gaussian Mixture Model$)$: 가우시안 분포를 기반으로 한 확률적 군집화 방법으로, 데이터를 여러 개의 가우시안 분포로 설명합니다.
7. 군집 수 결정
군집 분석을 할 때 가장 중요한 문제 중 하나는 적절한 군집 수를 결정하는 것입니다. 이를 위해 다음과 같은 방법을 사용합니다:
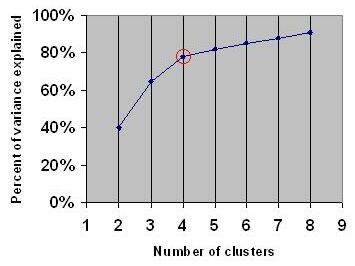
- 엘보우 방법 $($Elbow Method$)$: 군집 수를 늘렸을 때 응집도$($클러스터 내의 데이터 간의 유사도$)$의 변화를 관찰하고, 변화의 속도가 완만한 지점을 선택합니다.
- 실루엣 분석 $($Silhouette Analysis$)$: 클러스터 내 응집력과 군집 간 분리도를 종합적으로 평가하여 최적의 군집 수를 선택합니다.
- Gap Statistic: 실제 데이터와 무작위 생성 데이터를 비교하여 군집 수를 결정합니다.
8. 군집화 시각화
군집화 결과를 시각화하여 해석하는 것이 중요합니다. 다양한 시각화 방법을 사용하여 군집 결과를 이해하고 전달합니다:
- 산점도: 데이터 포인트를 그룹으로 나타내는 가장 기본적인 시각화 방법입니다.
- 클러스터 중심 시각화: 각 클러스터의 중심점을 시각화하여 클러스터의 특성을 파악합니다.
- 덴드로그램: 계층적 군집 분석 결과를 트리 형태로 시각화하여 데이터 간의 계층 구조를 보여줍니다.
- 히트맵: 데이터 포인트 간의 유사도를 색상으로 표현하여 클러스터 패턴을 파악합니다.
- t-SNE$($t-Distributed Stochastic Neighbor Embedding$)$: 고차원 데이터를 저차원으로 축소하여 시각화하여 데이터의 구조를 이해합니다.
'IT > AI' 카테고리의 다른 글
| [NLP] 자연어 처리: 트랜스포머 [기초] (0) | 2023.08.22 |
|---|---|
| [통계] Day 7-2 데이터 분석: 다변량 분석 (1) | 2023.08.22 |
| [통계] Day 6 데이터 분석: 차원 축소[PCA, 인자분석] (0) | 2023.08.22 |
| [통계] Day 5-2 시계열 데이터 분석 모델링 (0) | 2023.08.18 |