1. 시계열 데이터
시계열 데이터는 시간에 따라 기록된 데이터로, 주가, 기후, 판매량 등 다양한 분야에서 사용되며 중요한 정보를 제공합니다. 시계열 데이터 분석은 데이터의 패턴을 파악하고 미래 예측에 활용하는 중요한 기법입니다.
2. 시계열 데이터의 특성과 구성 요소
- 시간 의존성$($Time Depenency$)$
- 계절성$($Seasonality$)$
- 추세$($Trend$)$
- 자기 상관성$($Autocorrelation$)$
- 불규칙성$($Irregularity$)$
시계열 데이터는 다양한 패턴과 특성을 가지고 있습니다. 추세는 장기적인 증감 경향을 의미하며, 계절성은 일정한 주기마다 반복되는 변동을 의미합니다. 주기는 주기적으로 발생하는 변동을 나타내며, 불규칙성은 예측 모델에 포함되지 않는 예외적인 사건이나 임시적인 변동을 의미합니다. 이러한 구성 요소들을 이해하고 분석하는 것이 시계열 데이터 분석의 핵심입니다.
시계열 데이터의 변동성
- 분산$($Variance$)$: 데이터 값들의 퍼짐 정도를 나타내는 지표, 평균값과의 거리의 제곱의 평균
- 표준편차$($Standard Deviation$)$: 분산의 양의 제곱근
- 변동 계수$($Coefficient of Variation$)$: 표준편차를 평균으로 나눈 값, 상대적인 빈도를 나타내는 지표
시계열 데이터의 특성
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
# 1000일 분량의 임의 시간값
dates = pd.date_range(start="2023-08-17", periods=1000, freq="D")
values = np.random.randn(1000)
# 임의 시계열 데이터
data = pd.DataFrame({"Date": dates, "Value": values})
# ./data 폴더를 만든 뒤 csv로 저장
os.makedirs("./data", exist_ok=True)
data.to_csv("./data/sample_time_data.csv", index=False)
# csv 읽기: Date 칼럼은 미리 날짜값으로 인지해서 읽도록 지정
data = pd.read_csv("./data/sample_time_data.csv", parse_dates=["Date"], index_col="Date")
print(data)
print(type(data.index[0]))>>>
Value
Date
2023-08-17 -0.313167
2023-08-18 0.005767
2023-08-19 -0.388209
2023-08-20 0.936189
2023-08-21 1.369732
... ...
2026-05-08 -1.158711
2026-05-09 -1.997900
2026-05-10 1.465302
2026-05-11 0.018793
2026-05-12 0.100683
[1000 rows x 1 columns]
<class 'pandas._libs.tslibs.timestamps.Timestamp'>
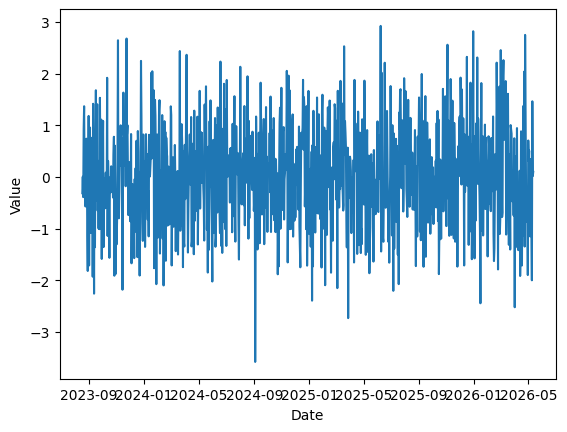
# x축: 시간값 (Date 칼럼, index_col로 지정했으므로 index로 호출)
plt.plot(data.index, data["Value"])
plt.xlabel("Date")
plt.ylabel("Value")
plt.show()>>>
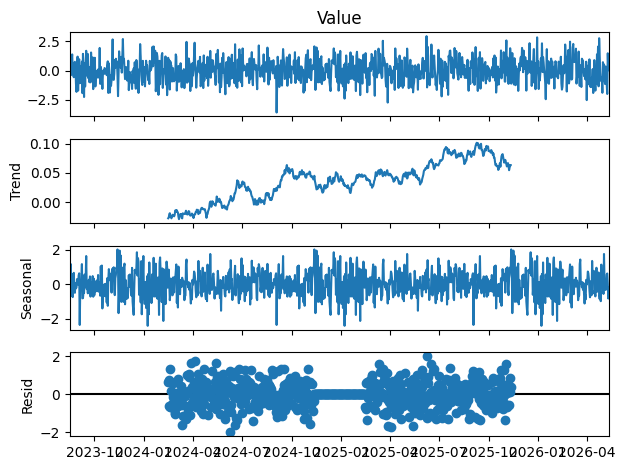
# 계절성 분해를 통한
result = seasonal_decompose(data["Value"], period=365)
result.plot()
plt.show()>>>
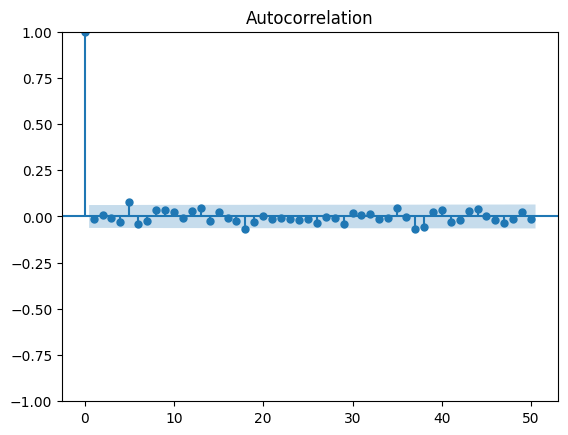
from statsmodels.graphics.tsaplots import plot_acf
# 자기상관성 분석 함수를 통한 그래프 작성
plt.figure()
plot_acf(data["Value"], lags=50)
plt.show()>>>
3. 시계열 데이터 분석 기법
- 이동 평균 $($Moving Average$)$
- 지수 평활법 $($Exponential Smoothing$)$
- ARIMA $($Autoregressive Integrated Moving Average$)$
- SARIMA $($Seasonal ARIMA$)$
- Prophet
- LSTM $($Long Short-Term Memory$)$
- VAR $($Vector Autoregression$)$
- 선형 회귀, 의사결정나무, 랜덤 포레스트 등의 기계학습 모델
시계열 데이터 분석은 다양한 기법을 활용하여 데이터의 패턴을 파악하고 미래 값을 예측하는데 활용됩니다. 각 기법은 데이터의 특성과 목적에 따라 선택됩니다.
4. 시계열 데이터의 시각화
- 선 그래프 $($Line Plot$)$
- 산점도 $($Scatter Plot$)$
- 히스토그램 $($Histogram$)$
- 박스 플롯 $($Box Plot$)$
- 히트맵 $($Heatmap$)$
- 자기 상관 그래프 $($Autocorrelation Plot$)$
시계열 데이터의 시각화는 데이터의 패턴과 특성을 파악하는데 중요한 역할을 합니다. 시계열 데이터를 그래프로 시각화하여 추세, 계절성, 주기 등을 파악할 수 있으며, 이를 통해 데이터의 특징을 더 잘 이해할 수 있습니다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
dates = pd.date_range("2023-01-01", periods=1000)
random_values = np.random.randn(1000)
cumsum_values = np.random.randn(1000).cumsum()
data = pd.DataFrame({
"Date": dates,
"Random_Value": random_values,
"Cumsum_Value": cumsum_values
})
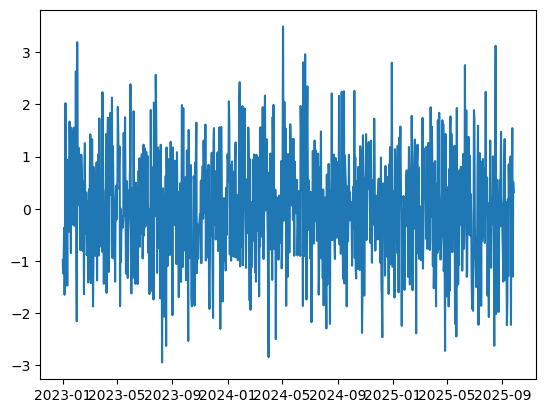
plt.plot(data["Date"], data["Random_Value"])
plt.show()
plt.figure()
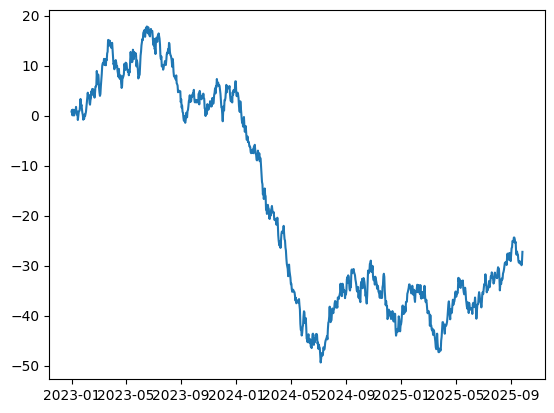
plt.plot(data["Date"], data["Cumsum_Value"])
plt.show()>>>
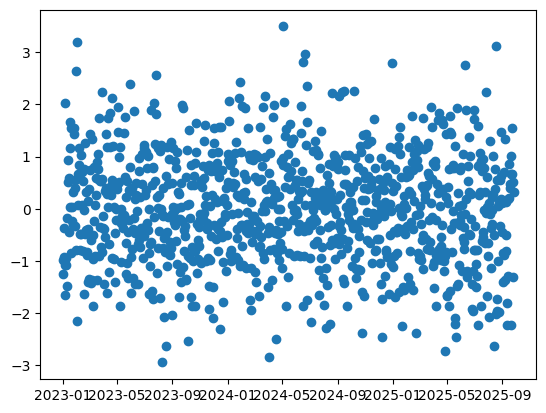
# 산점도
plt.figure()
plt.scatter(data["Date"], data["Random_Value"])
plt.show()
plt.figure()
plt.scatter(data["Date"], data["Cumsum_Value"])
plt.show()>>>
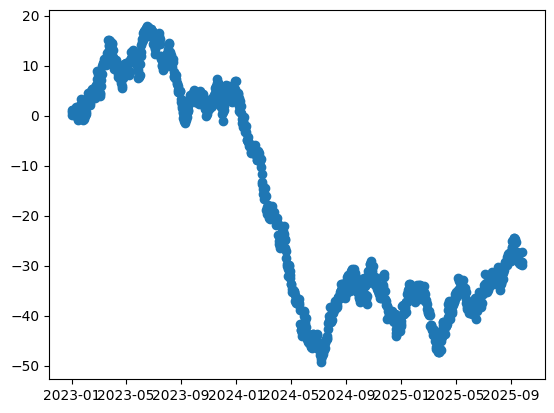
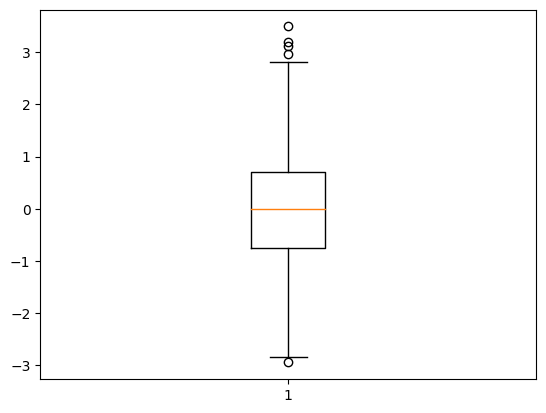
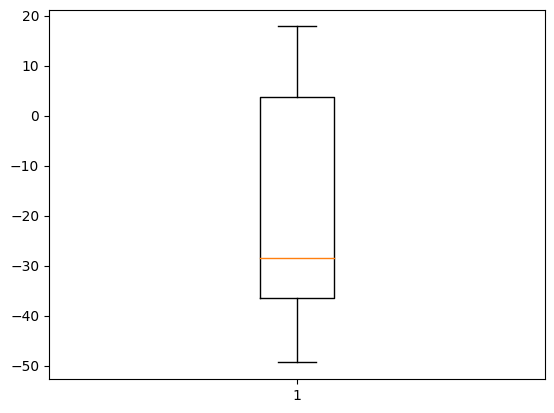
# 박스 플롯
plt.boxplot(data["Random_Value"])
plt.show()
plt.boxplot(data["Cumsum_Value"])
plt.show()>>>
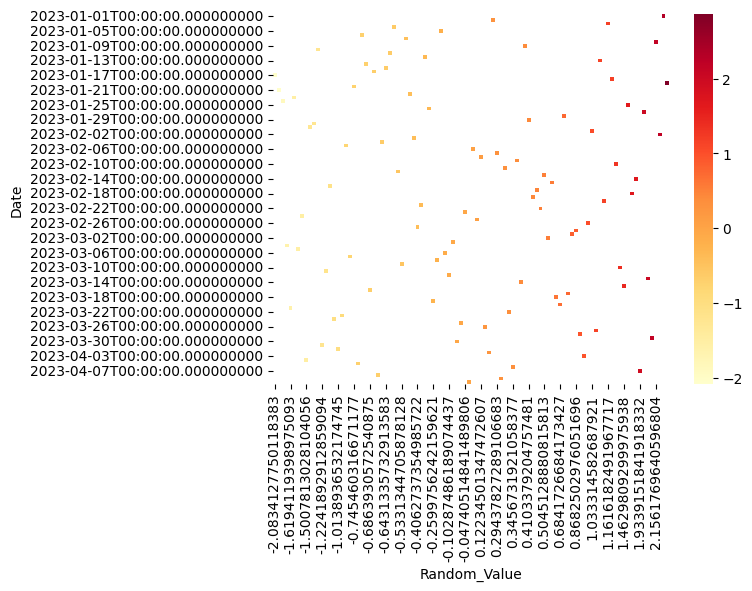
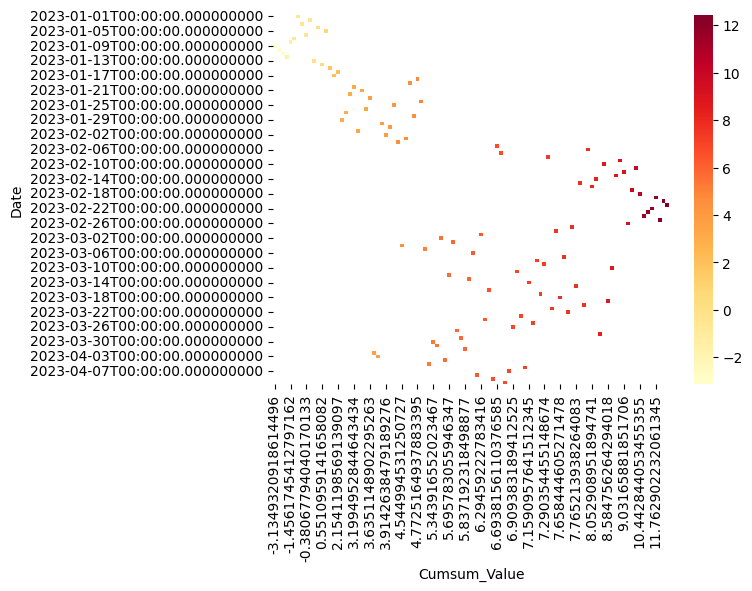
히트맵
import seaborn as sns
new_dates = pd.date_range(start="2023-01-01", periods=100)
new_values_random = np.random.randn(100)
new_values_cumsum = np.random.randn(100).cumsum()
new_data = pd.DataFrame({"Date": new_dates, "Random_Value": new_values_random, "Cumsum_Value": new_values_cumsum})
pivot_table_random = new_data.pivot(index="Date", columns="Random_Value", values="Random_Value")
pivot_table_cumsum = new_data.pivot(index="Date", columns="Cumsum_Value", values="Cumsum_Value")
sns.heatmap(pivot_table_random, cmap="YlOrRd", cbar=True)
plt.show()
sns.heatmap(pivot_table_cumsum, cmap="YlOrRd", cbar=True)
plt.show()>>>
5. 시계열 데이터 중요성
- 예측 및 추세 분석: 미래 값을 예측하고 데이터의 추세를 분석하여 의사 결정에 도움을 줍니다.
- 의사 결정 지원: 시계열 데이터를 분석하여 비즈니스 전략 수립 및 의사 결정을 지원합니다.
- 이상 탐지: 예상치 못한 변동이나 이벤트를 감지하여 조치를 취할 수 있습니다.
- 자원 할당과 계획: 시계열 데이터를 분석하여 자원을 효율적으로 할당하고 계획을 수립할 수 있습니다.
6. 시계열 분석의 목적
- 패턴 파악: 데이터의 주기성, 추세, 계절성 등 다양한 패턴을 파악하여 데이터의 특성을 이해합니다.
- 예측: 미래 값을 예측하여 수요 예측, 주가 예측 등에 활용합니다.
- 이상 탐지: 예상치 못한 변동을 감지하여 이상 현상을 조기에 파악하고 대응합니다.
- 인과 관계 파악: 시간적인 연관성을 분석하여 변수 간의 인과 관계를 이해합니다.
- 모델링과 통계 검증: 다양한 모델을 사용하여 데이터를 설명하고 예측하는 과정을 수행합니다. 통계적 검증을 통해 모델의 신뢰성을 평가합니다.
7. 시계열 분석의 활용 분야
- 금융 분석: 주가 예측, 자산 가치 평가, 금융 리스크 모델링, 금융 시계열 데이터의 패턴 분석 등에 활용됩니다.
- 수요 예측: 제품 수요 예측, 재고 관리, 고객 수요 분석 등에 활용됩니다.
- 자연재해 예측: 기상 이벤트, 태풍, 홍수 등 자연재해의 예측과 대응에 활용됩니다.
- 건강 관리: 질병 예측, 치료 효과 평가, 건강 상태 모니터링 등에 활용됩니다.
- 에너지 예측 및 최적화: 에너지 사용량 예측, 에너지 효율 개선, 전력 수급 예측 등에 활용됩니다.
- 교통 및 운송 분석: 교통량 예측, 교통 혼잡 예측, 운송 수요 예측 등에 활용됩니다.
- 경제 분석: 경기 변동 예측, 소비 동향 분석, 금리 변동 예측 등에 활용됩니다.
- 환경 모니터링: 대기 오염, 수질 오염, 기후 변화 등 환경 모니터링에 활용됩니다.
- 생산 공정 분석, 인구 예측, 마케팅 효과 분석, 품질 관리 등 다양한 분야에서 활용됩니다.
8. 주요 시계열 분석 기법
- 이동 평균$($Moving Average$)$: 시계열 데이터에서 주어진 기간의 평균을 계산하여 추세를 파악합니다.
- 지수 평활법$($Exponential Smoothing$)$: 이동 평균을 사용하여 추세를 예측하며, 최근 데이터에 가중치를 부여합니다.
- ARIMA$($Autoregressive Integrated Moving Average$)$: 자기회귀 누적 이동 평균 모델로 시계열 데이터의 자기상관성을 모델링하여 예측합니다.
- SARIMA$($Seasonal ARIMA$)$: ARIMA 모델에 계절성 요소를 추가하여 계절성을 고려한 예측을 수행합니다.
- Prophet: 페이스북에서 개발된 시계열 예측 라이브러리로, 트렌드와 계절성을 모델링하여 예측합니다.
- LSTM$($Long Short-Term Memory$)$: 딥러닝 모델 중 하나로, 장기 의존성을 가진 시계열 데이터 예측에 활용됩니다.
- VAR$($Vector Autoregression$)$: 다변량 시계열 데이터에 사용되며, 변수 간의 상호 관계를 모델링합니다.
- 선형 회귀, 의사결정나무, 랜덤 포레스트 등 다양한 기계 학습 알고리즘도 시계열 데이터 분석에 활용됩니다.
'IT > AI' 카테고리의 다른 글
| [통계] Day 4-3 시계열 데이터의 이상치 (0) | 2023.08.17 |
|---|---|
| [통계] Day 4-2 시계열 데이터 전처리 (0) | 2023.08.17 |
| [NLP] Word Embedding 기법 [기초] (0) | 2023.08.16 |
| [통계] Day 3-3 데이터 분포 가정과 가정 검토 (0) | 2023.08.16 |


