시계열 이상치
시계열 데이터에서 이상치란 다른 관측치들과 동떨어진 값으로, 잘못된 측정, 데이터 수집 오류, 자연적인 이벤트의 특이한 결과 등의 요인으로 발생합니다. 이상치는 데이터 분석과 예측에 부정적인 영향을 미칠 수 있으며, 이를 감지하고 처리하는 것이 중요합니다.
이상치 탐지
이상치 탐지는 데이터의 품질을 향상시키는 중요한 단계입니다. 이상치가 제거되지 않으면 모델의 정확성이 떨어지고, 예측 결과에 신뢰성이 떨어질 수 있습니다. 이상치 탐지는 데이터 분석에서 정확한 정보를 얻는 핵심 과정 중 하나입니다. 또한 이상치 패턴을 파악하여 이를 원인 분석에 활용할 수 있습니다.
방법
1. 이동 평균과 이동 표준 편차:
이동 평균은 데이터 포인트의 이전 N개의 포인트의 평균을 계산하는 방법입니다. 이동 표준 편차는 데이터 포인트의 이전 N개의 포인트의 표준편차를 계산합니다. 이 방법은 데이터의 변동을 고려하여 이상치를 감지하며, 이동 평균과 표준 편차 사이의 특정 비율을 기준으로 설정할 수 있습니다.
이동 평균 (Moving Average): \( MA_t = \frac{X_{t_{1}} + X_{t_{2}} + \ldots + X_{t_{N}}}{N} \)
이동 표준 편차 (Moving Standard Deviation): \( MSD_t = \sqrt{\frac{(X_{t_{1}} - MA_t)^2 + (X_{t_{2}} - MA_t)^2 + \ldots + (X_{t_{N}} - MA_t)^2}{N}} \)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
dates = pd.date_range("2023-08-17", periods=500)
values = np.random.randn(500)
data = pd.DataFrame({"Date": dates, "Value": values})
# 이동 평균 및 이동 표준편차 계산
WINDOW_SIZE = 7
moving = data["Value"].rolling(window=WINDOW_SIZE)
data["MovingAverage"] = moving.mean()
data["MovingStd"] = moving.std()
# 임계값 설정
threshold_multiplier = 2
data['Threshold_upper'] = data["MovingAverage"] + threshold_multiplier * data["MovingStd"]
data['Threshold_lower'] = data["MovingAverage"] - threshold_multiplier * data["MovingStd"]
# 이상치
data["Outlier"] = (data["Value"] > data['Threshold_upper']) | (data['Value'] < data['Threshold_lower'])
# 시각화
plt.figure(figsize=(16,6))
plt.plot(data["Date"], data["Value"], label="Value")
plt.plot(data["Date"], data["Threshold_upper"], color="green", label="Threshold_upper")
plt.plot(data["Date"], data["MovingAverage"], color="orange", label="MovingAverage")
plt.plot(data["Date"], data["Threshold_lower"], color="green", label="Threshold_lower")
plt.scatter(data[data["Outlier"]]["Date"], data[data["Outlier"]]["Value"], color='red')
plt.legend()
plt.show()>>>

2. 지수평활법:
지수평활법은 시계열 데이터의 추세와 계절성을 고려하여 데이터를 부드럽게 추정하는 방법입니다. 이 방법은 이전 데이터에 지수적인 가중치를 부여하며, 최근 데이터에 더 큰 가중치를 부여하여 이상치의 영향을 줄입니다.
\( \text{Forecast}_t = \alpha \times X_t + (1 - \alpha) \times (\text{Forecast}_{t_{1}} + T_{t_{1}}) \)
여기서, \( X_t \)는 현재 데이터, \( \alpha \)는 평활계수, \( \text{Forecast}_{t_{1}} \)은 이전 예측값, \( T_{t_{1}} \)은 이전 추세값입니다.
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing
dates = pd.date_range("2023-08-17", periods=100)
values = [10, 12, 11, 15, 9, 13, 8, 14, 10, 16] + [10] * 90
data = pd.DataFrame({"Date": dates, "Value": values})
model = ExponentialSmoothing(data["Value"], trend="add").fit()
# 지수 평활법 모델을 통한 추세 계산
trend = model.predict(start=0, end=len(data["Value"])-1)
# 위에서 계산된 추세와의 차이로 편차를 구함
deviation = data["Value"] - trend
# 이상치 기준
threshold = 2
outliers = abs(deviation) > threshold
# 시각화
plt.plot(data["Date"], data["Value"])
plt.plot(data["Date"], trend, color="orange")
plt.scatter(data[outliers]["Date"], data[outliers]["Value"], color="red")
plt.show()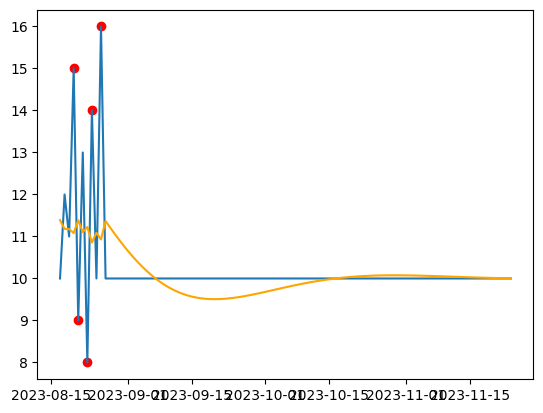
3. Z-score:
Z-score는 해당 데이터 포인트가 평균으로부터 몇 표준편차 맞큼 떨어져 있는지를 나타내는 값입니다. Z-score가 특정 임계값을 넘어서면 이상치로 판단할 수 있습니다.
\( Z = \frac{X_{\mu}}{\sigma} \)
여기서, \( X \)는 데이터 포인트, \( \mu \)는 평균, \( \sigma \)는 표준 편차입니다.
4. 스무딩:
스무딩은 데이터의 잡음이나 불규칙한 변동을 완화시키는 기법으로, 이상치의 영향을 줄이는 역할을 합니다. 이동 평균과 같은 스무딩 기법을 사용하여 데이터의 변동을 완화시키고 이상치를 탐지합니다. $($이동 평균의 수식과 동일$)$
5. 트렌드:
트렌드는 데이터가 장기적으로 증가하거나 감소하는 패턴을 의미합니다. 이 트렌드를 파악하여 데이터 포인트가 트렌드와 다른 경우 이상치로 판단할 수 있습니다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
dates = pd.date_range("2023-01-01", periods=100)
org_values = [10, 12, 11, 15, 9, 13, 8, 14, 10, 16]
values = []
for i in range(10):
values.extend(np.array(org_values) + (i + 1) * 2)
data = pd.DataFrame({"Date": dates, "Value": values})
result = seasonal_decompose(data["Value"], period=7)
plt.plot(data["Date"], data["Value"])
plt.plot(data["Date"], result.trend)
plt.show()>>>
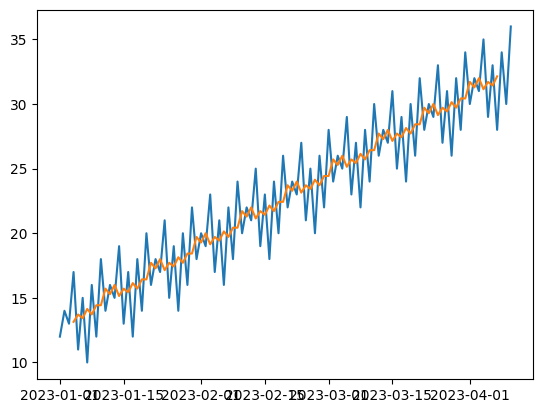
plt.plot(result.seasonal)
plt.show()>>>
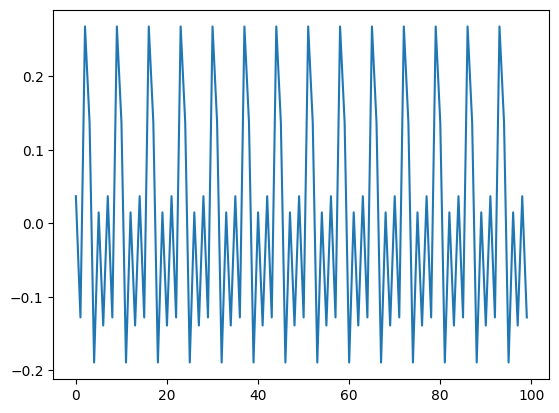
이상치 탐지는 다양한 분야에서 활용됩니다. 비즈니스 분석에서는 수요 예측, 재고 관리, 고객 분석 등에 활용될 수 있습니다. 또한 이상치 탐지를 통해 데이터의 이상한 패턴을 찾아 이를 원인 분석에 활용하여 문제 해결에 도움이 될 수 있습니다.
이상치 처리의 한계와 제약사항
- 이상치 정의의 주관성
- 이상치 감지/탐지의 어려움
- 이상치 처리의 영향 $($왜곡의 가능성$)$
- 시계열 데이터의 복잡성
- 대량의 데이터 처리의 어려움
'IT > AI' 카테고리의 다른 글
| [통계] Day 5-2 시계열 데이터 분석 모델링 (0) | 2023.08.18 |
|---|---|
| [통계] Day 5-1 시계열 데이터의 정규화 (0) | 2023.08.18 |
| [통계] Day 4-2 시계열 데이터 전처리 (0) | 2023.08.17 |
| [통계] Day 4-1 시계열 데이터 분석 (0) | 2023.08.17 |


