1. 정규화 변환의 필요성
- 데이터 스케일 조정의 중요성: 다양한 변수의 값 범위를 조정하여 모델이 각 변수에 공정하게 영향을 받도록 함.
- 정규 분포 가정과 그 효과: 정규 분포를 따르는 데이터로 변환하여 통계적 분석을 용이하게 함.
- 이상치 처리와의 관련성: 이상치가 정규화에 영향을 줄 수 있으며, 변환 후 이상치의 영향을 줄이기 위해 사용.
- 시계열 패턴 강조와 모델 안정성: 시계열 패턴을 더 잘 드러나게 하며 모델의 안정성과 예측 성능 향상을 도모.
2. 주요 정규화 변환 방법
- 최소-최대 정규화 $($Min-Max Normalization$)$: 데이터 값을 최소값과 최대값 사이의 범위로 변환, 이상치에 민감하지 않은 경우 사용.
$X_{\text{new}} = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}}$
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
dates = pd.date_range("2023-01-01", periods=100)
values = np.random.randint(0, 100, size=100)
data = pd.DataFrame({"Date": dates, "Value": values})
plt.plot(data["Date"], data["Value"])
plt.show()
min_value = data["Value"].min()
max_value = data["Value"].max()
data["Value_Normalized"] = (data["Value"] - min_value) / (max_value - min_value)
plt.plot(data["Date"], data["Value_Normalized"])
plt.show()
- z-점수 정규화 $($Z-Score Normalization$)$: 평균을 0, 표준편차를 1로 조정하여 데이터 분포를 표준 정규분포에 가깝게 변환.
$X_{\text{new}} = \frac{X - \text{mean}}{\text{std}}$
- 로그 변환 $($Log Transformation$)$: 로그 함수를 적용해 비선형적인 패턴을 선형적으로 변환, 왜도가 높은 데이터나 비데칭 분포를 보정.
$Y = \ln(X)$
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.DataFrame({"Value": [2 ** i for i in range(10)]})
# 로그 변환
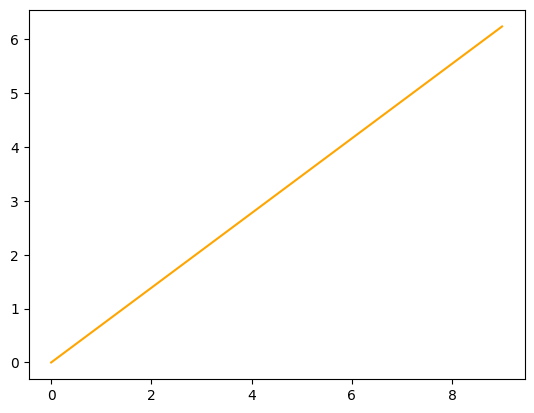
data["LogValue"] = np.log(data["Value"])
plt.plot(data["Value"], color='blue')
plt.show()
plt.plot(data["LogValue"], color='orange')
plt.show()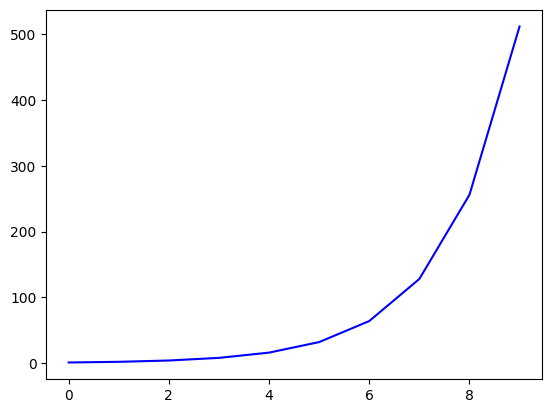
- 차분$($Differencing$)$: 현재 관측값과 이전 관측값 간의 차이를 계산하여 추세나 계절성 제거, 데이터의 패턴에 집중, 불규칙성 제거, 정상성$($stationarity$)$를 갖는 시계열 데이터로 변환.
i차 차분 := $\text{Diff}_{t} = X_{t} - X_{t-i}$
import pandas as pd
import matplotlib.pyplot as plt
data = pd.DataFrame({"Value": [10, 20, 30, 40, 50]})
data["DiffValue"] = (data["Value"]).diff()
plt.plot(data["Value"])
plt.show()
plt.plot(data["DiffValue"])
plt.show()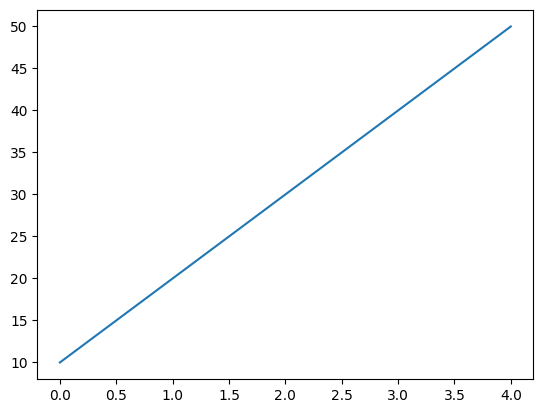

- 박스-콕스 변환$($Box-Cox Transformation$)$: 양수인 데이터의 정규화, 최대 우도 추청$($maximum likelihood estimation$)$을 사용하여 변환 파라미터$($lambda$)$를 적용.
$Y_{\lambda} = \begin{cases} \frac{X^{\lambda}-1}{\lambda} & \lambda \neq 0 \\ \log_{e}X\end{cases}$
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
data = pd.DataFrame({"Value": [10, 100, 1000, 10000, 100000]})
# lambda는 python에 내장도니 키워드이기 때문에 (람다 함수) 변수명으로 사용할 수 없음에 주의
transformed_data, lmbda = stats.boxcox(data["Value"])
print(transformed_data)
print(f"최적 람다값: {lmbda:.4f}")
>>>
[ 2.30258283 4.60516112 6.90773489 9.21030413 11.51286883]
최적 람다값: -0.0000plt.plot(data["Value"])
plt.title("Original plot")
plt.show()
plt.plot(transformed_data)
plt.title("Box-Cox transformed plot")
plt.show()

3. 고려해야 할 사항
- 데이터 분포의 형태와 선택의 중요성: 데이터 분포의 모양에 따라 적절한 변환 방법을 선택하여 데이터를 정규화해야 함.
- 변수 간 스케일의 조정 방법: 변수 간 스케일이 다르면 같은 비중을 부여하기 위해 정규화나 표준화를 사용해야 함.
- 이상치의 영향과 처리 전략: 이상치가 변환에 영향을 줄 수 있으므로 이상치 처리 후에 정규화를 고려해야 함.
- 변수 간 상관 관계와 변환: 변수 간 상관 관계가 높은 경우 변환을 통해 다중 공선성 문제를 완화시킬 수 있음.
- 분석 목적에 따른 변환 선택 가이드: 분석 목적과 예측 모델 종류에 따라 적합한 변환 방법을 선택해야 함.
4. 데이터의 특성과 분석 목적에 따른 선택 가이드 제시
- 데이터 분포의 형태에 따른 선택:
- 정규분포를 따를 경우: 정규화나 표준화를 적용하여 데이터를 변환할 수 있습니다.
- 비정규분포를 따를 경우: 로그 변환, 박스-콕스 변환 등 비선형 변환을 고려하여 데이터 분포를 보정할 수 있습니다.
- 스케일의 조정:
- 변수 간 스케일이 다른 경우: 정규화나 표준화를 활용하여 변수들을 동일한 스케일로 조정할 수 있습니다.
- 이상치의 처리:
- 이상치가 존재하는 경우: 이상치를 제거하거나 대체한 후에 정규화나 변환을 적용하여 분석에 활용할 수 있습니다.
- 변수 간 상관 관계와 시계열 패턴:
- 변수 간 상관 관계가 높은 경우: 차분, 로그 변환 등을 활용하여 변수 간 상관 관계를 줄일 수 있습니다.
- 시계열 데이터의 특성: 트렌드나 계절성을 갖는 데이터인 경우에는 변환 방법을 고려할 때 이를 고려하여 선택할 수 있습니다.
5. 결과 해석에 대한 고려
- 정규화나 표준화를 적용한 경우:
- 해석이 용이하고 변수 간의 상대적인 영향력을 비교하기 용이합니다.
- 각 변수의 값 범위가 동일하게 조정되어 모델의 안정성을 향상시킬 수 있습니다.
- 비선형 변환을 적용한 경우:
- 원래 데이터와의 관계를 해석할 때 주의가 필요합니다.
- 변환된 데이터의 해석이 원 데이터와 다를 수 있으며, 이를 고려하여 분석 결과를 해석해야 합니다.
- 분석 목적에 따른 선택:
- 선형 회귀 분석: 변수 간의 관계를 분석하고 예측할 때 정규화나 표준화를 활용할 수 있습니다.
- 시계열 분석: 시계열 패턴을 분석할 때 차분, 로그 변환 등을 사용하여 데이터를 변환하여 패턴을 파악할 수 있습니다.
'IT > AI' 카테고리의 다른 글
| [통계] Day 6 데이터 분석: 차원 축소[PCA, 인자분석] (0) | 2023.08.22 |
|---|---|
| [통계] Day 5-2 시계열 데이터 분석 모델링 (0) | 2023.08.18 |
| [통계] Day 4-3 시계열 데이터의 이상치 (0) | 2023.08.17 |
| [통계] Day 4-2 시계열 데이터 전처리 (0) | 2023.08.17 |


